Ce portail contient du matériel qui couvre trois objectifs principaux divisés en : recherche, enseignement et développement de logiciels:






Le projet de recherche: Méthodes de fonctions de base radiale pour la solution de EDPs, a pour objectif premier d'étudier, rechercher et développer de nouveaux algorithmes numériques basés sur la théorie des fonctions de base radiales pour la solution de Èquations aux Dérivées Partielles (EDP). Ces techniques, développées au cours de cette dernière décennie, constituent un outil puissant pour résoudre des problèmes réels à grande échelle. De par sa nature, ce projet est interdisciplinaire puisque son objectif inclut également la modélisation mathématiques de problèmes abordant différents domaines de connaissances.
Un autre objectif important de ce projet est d'élaborer une bibliothèque de codes informatiques permettant d'implémenter ces méthodes. Il ne s’agit pas seulement d'utiliser des “boîtes noires” pour résoudre des problèmes d'EDP, mais de renforcer la recherche et le développement de systèmes numériques et informatiques pour ces nouvelles méthodes.
Dans ce domaine, nous avons l’intention de réaliser des recherches tant dans le domaine de méthodes numériques appliquées que dans des domaines appartenant à différentes disciplines.
Nous avons inclu des documents et des codes informatiques introductifs ainsi que des explications, qui visent à aider autant les professeurs que les étudiants qui étudient et/ou enseignent dans ce domaine.
Le troisième objectif est celui de construire une bibliothèque de programmes libres dont la flexibilité permet à l'utilisateur d'intégrer de nouvelles routines ou des algorithmes.
(Méthodes numériques pour la solution d'équations aux dérivées partielles : une critique)
Bien que les méthodes des fonctions radiales de base radiales servant à la résolution d'EDP aient été développées dans les années 1990, leur impact est resté dans les communautés des ingénieurs et des mathématiciens (voir [I, II, III, IV, V , VI] et les références qui y sont contenues). L’absence de mailles pour l’élaboration de ces schémas numériques explique en grande partie le succès de ces techniques. En simulations réelles, il est fréquent que 70% du temps de traitement soit dû à la génération de mailles. Dans ce contexte, nous remarquons les éléments suivants qui font que ces méthodes sont plus puissantes que les méthodes classiques :
Aucune de ces méthodes ne requiert une construction de mailles, élément qui réduit considérablement la complexité algorithmique de ces méthodes. Il existe des stratégies simples pour affiner le nombre de nœuds dans les régions où la fonction présente des oscillations et des gradients élevés. En comparaison, les techniques de nœuds adaptés sont beaucoup moins coûteuses que les algorithmes de mailles adaptées.
Le traitement des problèmes de dimensions supérieures à deux et avec des frontières complexes a des résultats plus simples et efficaces qu'avec des méthodes dépendants de mailles.
Il existe plusieurs façons de classer les méthodes numériques de fonctions radiales de base pour la solution d'équations différentielles partielles. En particulier, elles peuvent être regroupées en deux catégories :
• Méthodes de base radiale:
→ Méthodes globales
→ Méthodes locales
• Méthodes des moindres carrés mobiles
Ce qui distingue ces deux approches est que, dans le cas des méthodes de base radiale, l'ordre de convergence du schéma dépend du type de noyau de base radial, alors que pour les méthodes des moindres carrés mobiles, même quand le noyau est radial, l'ordre de convergence est déterminé par la technique des moindres carrés. En d'autres termes, les méthodes de base radiales héritent de l'ordre de convergence du noyau radial qui le détermine, qui peut être de type exponentiel, alors que les méthodes de moindres carrés mobiles ont un ordre de convergence algébrique indépendant du noyau radial utilisé.
Une autre différence importante est que les méthodes de base radial sont invariantes par rapport à la dimension de l'espace, c'est-à-dire que la nature radiale de la méthode fait que le système algébrique de Gramm correspond à la méthode ayant la même complexité numérique en une, deux ou plus dimensions. En revanche, les méthodes de moindres carrés mobiles, dont la caractérisation dépend d'un réglage numérique, ont une complexité numérique dépendant de la dimension de l'espace euclidien.
D'un autre côté, les méthodes globales de type radial dérivent d'un système algébrique unique d'équations incluant tous les nœuds du domaine, alors que les méthodes des moindes carrés mobiles nous conduisent à un ensemble de systèmes algébriques relativement petits par rapport au nombre total de nœuds. Simultanément, alors que les méthodes de moindres carrés mobiles sont consistants à l'EDP, les méthodes basés en noyaux radiaux en reproduisent pas nécessairement des polynômes et en sont donc pas consistants à l'EDP.
Dans le cas des méthodes globales de fonctions de base radiale, un des principaux problèmes est que le conditionnement de la matrice du système augmente lorsque le nombre de nœuds augmente. Cela en s eproduit pas dans le cas des méthodes de MLS, étant donné que les systèmes locaux en permettent pas de construire des matrices bandes et à diagonales dominantes. Les méthodes locales, cependant, ne peuvent pas gémérer des schémas convergeants exponentiellement, tandis que les globales le peuvent. De plus, il a été développé, pour les méthodes globales, des techniques de décomposition de domaine et de préconditionnement, qui permettent de résoudre des problèmes pour un grand nombre de nœuds.
Les deux approches ont eu un impact important dans différentes disciplines et sont efficacité pour résoudre différents problèmes est une question qui fait l'objet de la recherche actuelle. Parmi les méthodes de ces deux groupes, les plus importantes sont :
Méthodes de base radiale:
• Emplacement symétrique et asymétrique
• Quadrature différentielle
• Méthodes de fonctions radiale à support compact
• Méthodes de solutions fondamentales
Méthodes de moindres carrés mobiles:
• Petro Galerkin sans maille (MLPG)
• Elements finis par partition de l'unité (PUFEM)
• Noyaux reproduits par partition de l'unité (RKPM)
• Hydrodynamique de particules lisses (SPH)
Dans un travail récent, Fasshauer [VII] a introduit une formulation abstraite unifiant les deux approches – pour le cas des noyaux radiaux – dans un cadre commun. En particulier, l'auteur a démontré que les méthodes locales obtenues par les moindres carrés peuvent se transformer en méthodes globales lorsque le nombre de nœuds du support des techniques locales entourent tous les nœuds du domaine.
[I] S. N. Atluri and S. Shen, The Meshless Local Petrov-Galerkin (MLPG) Method, Tech Science Press, Encino, CA, 2002.
[II] M. D. Buhmann, Radial Basis Functions : Theory and Implementations, Cambridge University Press, Cambridge, 2003.
[II] E. W. Cheney and W. A. Light, A Course in Approximation Theory, Brooks/Cole, Pacific Grove, CA, 1999.
[IV] G. R. Liu, Mesh Free Methods: Moving beyond the Finite Element Method, CRC Press, Boca Raton, FL, 2002.
[V] Wendland, H., Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge, UK., 2005
[VI] G. E. Fasshauer, Meshfree Approximation Methods with Matlab Interdisciplinary Mathematical Sciences - Vol. 6 World Scientific Publishers, Singapore, 2007
[VII] G. E. Fasshauer, Dual Bases and Discrete Reproducing Kernels: A Unified Framework for RBF and MLS Approximation, Engineering Analysis with Boundary Elements, Volume 29, Issue 4, April 2005, pages 313-325
II Apliccation des méthodes de RBF dans différentes disciplines:
1. Mathématiques financières:
L'équation différentielle partielle de Black-Scholes a été fréquemment utilisée pour la modélisation des prix des contrats financiers. Les modèles d'option de tarification en une dimension pour les options américaines et européennes ont été explorées par des méthodes de RBF, par Hon et al. [1,2] et en deux dimensions par Fasshauer et al [3] et par Marcozzi et al. [4]. Ils ont formulé une méthode basée sur des fonctions quasi-radiales en une dimension [5]. Récemment, Petterson et al. [6] ont résolu le problème multi-dimensionnel pour l'option européenne basket call par une méthode d'emplacement asymétrique avec noyau multiquadratique et noeuds adaptés, reportant que ses résultats sont de 20 à 40 fois plus rapides que les résultats obtenus avec des différences finies adaptées.
[1] Y.-C. Hon, X.-Z. Mao, A radial basis function method for solving options pricing models, J. Financial Engineering 8 (1999) 31–49.
[2] Z.Wu, Y.-C. Hon, Convergence error estimate in solving free boundary diffusion problem by radial basis functions method, Engrg. Anal. Bound. Elem. 27 (2003) 73–79.
[3] G. E. Fasshauer, A. Q. M. Khaliq, D. A. Voss, Using meshfree approximation for multi-asset American option problems, J. Chinese Institute Engineers 27 (2004) 563–571.
[4] M. D. Marcozzi, S. Choi, C. S. Chen, On the use of boundary conditions for variational formulations arising in financial mathematics, Appl. Math. Comput. 124 (2001) 197–214.
[5] Y. C. Hon, A quasi-radial basis functions method for American options pricing, Comput. Math. Appl. 43 (3) (2002) 513–524.
[6] Ulrika Pettersson, Elisabeth Larsson, Gunnar Marcusson, and Jonas Persson, Improved Radial Basis Function Methods for Multi-Dimensional Option Pricing, Technical Report 2006-028, Uppsala University, 2006.
Dans [7], N. Flyer et al, le problème de la modélisation du mouvement des flux géophysiques se déplaçcant dans une sphère dominée par des limites connectées est posé. Ceci est le premier ouvrage dans lequel sont résolues des équations différentielles partielles hyperboliques grâce aux fonctions de base radiale. Les auteurs rapportent que le nombre de noeuds requis est inférieur que celui utilisé par des méthodes spectrales. De plus, la méthode RBF permet de passer plus de temps pour obtenir la même précision que celles utilisés par les méthodes spectrales classiques.
Dans Jichun Li [8] , Hon [9] et Wong et al. [10], les équations pour les dépôts en eau peu profonde (shallow water equations) sont résolues par la méthode de placement asymétrique avec noyau multiquadratique, En particulier, dans [20], une étude est réalisée pour le port de Tolo et HongKong, qui est comparée avec des techniques d'éléments finis et des données de terrain, reportées par des supérieurs sur la technique des EF et une excellente coïncidence avec ces données.
[7] N. Flyer and G.B. Wright, Transport schemes on a sphere using radial basis functions. J. Comp. Phys., to appear (2007).
[8] Jichun Li, C.S. Chen, Darrel Pepper, Yitung Chen, "Mesh-free method for groundwater modeling", Boundary Elements XXIV, eds. C.A. Brebbia, A. Tadeu and V. Popov, WIT Press, Southampton, Boston, pp. 115-124 (2002).
[9] Y. C. Hon, K. F. Cheung, X. Z. Mao, and E. J. Kansa, .A Multiquadric Solution for Shallow Water Equations", ASCE J. Hydraulic Engineering, 125, (5), 524-533 (1999).
[10] Wong, S. M., Hon, Y. C., and Golberg, M. A. 2002. Compactly supported radial basis functions for shallow water equations. Appl. Math. Comput. 127, 1 (Mar. 2002), 79-101
La modélisation des écoulements diphasiques et triphasiques est abordée par Hon dans [11] et [12] en utilisant une approche de placement asymétrique eulérien utilisant des multiquadriques. A. Iske et coll. [13] [14] abordent le même problème en développant une méthode semi-lagrangienne qui utilise des noyaux de plaques minces pour la solution des équations de Buckley-Leverett, afin de modéliser des problèmes en deux phases applicables à la récupération primaire des puits en l'industrie pétrolière.
[11] Y. C. Hon, M. W. Lu, W. M. Xue, and X. Zhou, "Multiquadric Method for the Numerical Solution of a Biphasic Model", Internat. J. Appl. Sci. Comput., 88, 153-175 (1997).
[12] Y. C. Hon , M. Lu , M. W. Xue and X. Zhou, "Numerical Algorithm for Triphasic Model of Charged and Hydrated Soft Tissues", Computacional Mechanics, 29(1), , pp 1-15 (2002)
[13] A. Iske and M. Käser: Two-Phase Flow Simulation by AMMoC, an Adaptive Meshfree Method of Characteristics. Computer Modeling in Engineering & Sciences (CMES) 7(2), 2005, 133-148.
[14] J. Behrens, A. Iske, and M. Käser: Adaptive Meshfree Method of Backward Characteristics for Nonlinear Transport Equations, in Meshfree Methods for Partial Differential Equations, M. Griebel and M. A. Schweitzer (eds.), Springer-Verlag, Heidelberg, 2002, 21-36.
Chen et coll. [15] étudient la modélisation du transport des contaminants pour les réservoirs d'eau à l'aide de techniques de placement RBF. L'étude
Le numérique comprend plusieurs cas : diffusion pure, advection et dispersion pour une source continue, advection et dispersion pour une source instantanée.
[15] J. Li, Y. Chen and D. Pepper, Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling, Computational Mechanics, (32) 10-15, 2003
La solution de l'équation de Navier Strokes, tant stationnaire que dépendante du temps, a été abordé par Shu, et al. [16] [17] [18], où se résoud le problème de la cavité carrée, Ghia, grâce à la méthode de quadrature différentielle pour les nombre de Reinolds de 10^5.
[16] Shu, C., Khoo, B. C., and Yeo, K. S. 1994. Numerical solutions of incompressible Navier—Stokes equations by generalized differential quadrature. Finite Elem. Anal. Des. 18, 1-3 (Dec. 1994), 83-97.
[17] C. Shu, H. Ding and K. S. Yeo (2005), 'Computation of incompressible Navier-Stokes equations by local RBF-based differential quadrature method', CMES-Computer Modeling in Engineering and Sciences, 7, 195-205.
[18] H. Ding, C. Shu, K. S. Yeo and D. Xu (2006), 'Numerical Computation of Three-dimensional Incompressible Viscous Flows in the Primitive Variable Form by Local Multiquadric Differential Quadrature Method', Computer Methods in Applied Mechanics and Engineering, 195, 516-533.
Chinchapatnam et al. [19] ont recherché l'équation non stationnaire de convection diffusion en une ou deux dimensions pour différents nombres de Peclet par un placement symétrique et asymétrique. Le schéma numérique utilise des fonctions radiales globales, telles que les multiquadratiques, multiquadratiques inverses, splines en plaque mince et d'ordre 5. Dans cette étude comparative, les auteurs ont conclu que la méthode symétrique est meilleure que l'asymétrique, et que pour des grands nombres de Peclet il recquièrent une forte densité de noeuds pour obtenir une bonne approximation.
[19] Chinchapatnam, P.P., Djidjeli, K and Nair, P.B. (2006). Unsymmetric and symmetric meshless schemes for the unsteady convection–difusión equation. Computer Methods in Applied Mechanics and Engineering, 195, (19-22), 2432-2453.
Il existe peu de références, aussi loin que nous le savons, sur les algorithmes basés sur les fonctions radiales globales qui résolvent des problèmes d'analyse structurale. , le travail de Ferreira et al. [20] qui aborde le problème des efforts de poutres et plaques déformables, ainsi que le travail de Zhang et al. [21] sur l'élasticité plane. Récemment, Tiago et al. [22] utilisent la méthode de placement asymétrique avec des noyaux radiaux distincts pour résoudre et analyser les problèmes à une dimension comme des problèmes d'élasticité linéaire statique, de vibration libre et analyse linéaire de stabilité, pour des problèmes physiqes non-linéaires de modèles endommagés.
[20] A. J. M. Ferreira, C. M. C. Roque, and P. A. L. S. Martins. Radial basis functions and higher-order shear deformation theories in the analysis of laminated composite beams and plates. Composite Structures, 66(1–4):287–293, 2004.
[21] X. Zhang, K. Z. Song, M. W. Lu, and X. Liu. Meshless methods based on collocation with radial basis functions. Computational Mechanics, 26(4):333–343, 2000.
[22] C. Tiago and V. Leitão, Application of radial basis functions to linear and non-linear structural analysis problems, Computers & Mathematics with Applications, 51(8), 1311-1334, 2006.
Méthodes numériques pour résoudre les EDP par les RBF
• Placement symétrique et asymétrique
• Quadrature différentielle
• Galerkin.
• Méthodes de préconditionnement
• Décomposition des domaines
→ Algorithme avec traslepe
→ Algorithme sans traslepe
• Algorithmes de nœuds adaptés
→ Algorithmes locaux
→ Algorithmes globaux
• Visualisation des solutions
Flux de phase non miscible. Equation de Buckley Leverett
Modélisation du transport des contaminants de l’eau d'un réservoir
Comme nous l'avons mentionné dans la page principale, un objectif important de ce projet est de construire une bibliothèque de logiciels permettant d'implémenter des algorithmes sur les fonctions de base radiales pour la solution d'EDP. Un objectif majeur de ce point-là est de permettre à l'utilisateur d'inclure d'une manière facile de nouveaux modules et procédures par l'intermédiaire d'une stratégie de programmation par objet en C++.
La bibliothèque est actuellement au stade initial, nous invitons les développeurs de logiciels intéressés par ce domaine à ajouter des modules orientés objet suivant l'approche du logiciel libre (licence GPL). Pour cela, contactez Daniel A, Cervantes pour toute question liée à cette bibliothèque,
| LA::Matrix | Base class for matrices |
| LA::Point | Base class for Points |
| LA::Point2dT | Class for two dimension points |
| LA::Point3dT | Class for three dimension points |
| RBF::GramMatrix | Gram matrix class |
| RBF::MQ | Multicuadric kernel 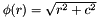 |
| RBF::TPS2 | Second order thin plate spline kernel 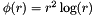 |
| RBF::TPS4 | Fourth order thin plate spline kernel 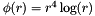 |
| RBF::TPS_2DX | Second order partial derivative of thin plate spline (with respect to 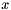 ) ) |
| RBF::TPS_2DY | Second order partial derivative of thin plate spline (with respect to 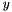 ) ) |
| RBF::TPSInterp | Thin plate spline interpolator class |
RBF++-0.1/examples/linear_alg/linear_alg.cpp [code] RBF++-0.1/examples/tps_interpolation/tps_interpolation.cpp [ code] RBF++-0.1/examples/tps_poisson/tps_poisson.cpp [code] RBF++-0.1/include/LA/Matrix.h [code] RBF++-0.1/include/LA/Point.h [code] RBF++-0.1/include/LA/Point2dT.h [code] RBF++-0.1/include/LA/Point3dT.h [code] RBF++-0.1/include/RBF/GrammMatrix.h [code] RBF++-0.1/include/RBF/RBF.h [code] RBF++-0.1/include/RBF/TPSInterp.h [code] RBF++-0.1/src/LA/Matrix.cpp [code] RBF++-0.1/src/LA/Point.cpp [code] RBF++-0.1/src/RBF/GrammMatrix.cpp [code] RBF++-0.1/src/RBF/TPSInterp.cpp [code]
Dans [7], N. Flyer et al. Le problème de la modélisation du mouvement des écoulements géophysiques dans une sphère dominée par des termes connectifs est posé. Il s'agit de
Le premier travail dans lequel des équations aux dérivées partielles hyperboliques sont résolues à l'aide de fonctions de base radiales. Les auteurs rapportent que le nombre de nœuds requis est bien inférieur à celui utilisé par les méthodes spectrales. De plus, la méthode RBF permet des pas de temps beaucoup plus longs pour obtenir la même précision que ceux utilisés par les méthodes spectrales classiques.
Dans Jichun Li [8], Hon [9] et Wong et al. [10] les équations pour les réservoirs d'eau peu profonde (équations d'eau peu profonde) sont résolues à l'aide de la méthode
placement asymétrique avec noyaux multiquadriques. En particulier, dans [20] une étude est réalisée pour les ports de Tolo et HonKong, qui est comparée à
techniques d'éléments finis et de données de terrain, rapportant une supériorité sur la technique FE et une excellente coïncidence avec les données de terrain.
[7] N. Flyer and G.B. Wright, Transport schemes on a sphere using radial basis functions. J. Comp. Phys., to appear (2007).
[8] Jichun Li, C.S. Chen, Darrel Pepper, Yitung Chen, "Mesh-free method for groundwater modeling", Boundary Elements XXIV, eds. C.A. Brebbia, A. Tadeu and V. Popov, WIT Press, Southampton, Boston, pp. 115-124 (2002).
[9] Y. C. Hon, K. F. Cheung, X. Z. Mao, and E. J. Kansa, .A Multiquadric Solution for Shallow Water Equations", ASCE J. Hydraulic Engineering, 125, (5), 524-533 (1999).
[10] Wong, S. M., Hon, Y. C., and Golberg, M. A. 2002. Compactly supported radial basis functions for shallow water equations. Appl. Math. Comput. 127, 1 (Mar. 2002), 79-101
La modélisation des écoulements diphasiques et triphasiques est abordée par Hon dans [11] et [12] en utilisant une approche de placement asymétrique eulérien utilisant des multiquadriques. A. Iske et coll. [13] [14] abordent le même problème en développant une méthode semi-lagrangienne qui utilise des noyaux de plaques minces pour la solution des équations de Buckley-Leverett, afin de modéliser des problèmes en deux phases applicables à la récupération primaire des puits en l'industrie pétrolière.
[11] Y. C. Hon, M. W. Lu, W. M. Xue, and X. Zhou, "Multiquadric Method for the Numerical Solution of a Biphasic Model", Internat. J. Appl. Sci. Comput., 88, 153-175 (1997).
[12] Y. C. Hon , M. Lu , M. W. Xue and X. Zhou, "Numerical Algorithm for Triphasic Model of Charged and Hydrated Soft Tissues", Computacional Mechanics, 29(1), , pp 1-15 (2002)
[13] A. Iske and M. Käser: Two-Phase Flow Simulation by AMMoC, an Adaptive Meshfree Method of Characteristics. Computer Modeling in Engineering & Sciences (CMES) 7(2), 2005, 133-148.
[14] J. Behrens, A. Iske, and M. Käser: Adaptive Meshfree Method of Backward Characteristics for Nonlinear Transport Equations, in Meshfree Methods for Partial Differential Equations, M. Griebel and M. A. Schweitzer (eds.), Springer-Verlag, Heidelberg, 2002, 21-36.
Chen et coll. [15] étudient la modélisation du transport des contaminants pour les réservoirs d'eau à l'aide de techniques de placement RBF. L'étude numérique comprend plusieurs cas : diffusion pure, advection et dispersion pour une source continue, advection et dispersion pour une source instantanée.
[15] J. Li, Y. Chen and D. Pepper, Radial basis function method for 1-D and 2-D groundwater contaminant transport modeling, Computational Mechanics, (32) 10-15, 2003
La solution de l'équation de Navier Stokes, à la fois stationnaire et dépendante du temps, a été abordée par Shu et al. [16] [17] [18], où
résout le problème de la cavité carrée, Ghia, en utilisant la méthode de quadrature différentielle pour les nombres de Reinolds de 10^5.
[16] Shu, C., Khoo, B. C., and Yeo, K. S. 1994. Numerical solutions of incompressible Navier—Stokes equations by generalized differential quadrature. Finite Elem. Anal. Des. 18, 1-3 (Dec. 1994), 83-97.
[17] C. Shu, H. Ding and K. S. Yeo (2005), 'Computation of incompressible Navier-Stokes equations by local RBF-based differential quadrature method', CMES-Computer Modeling in Engineering and Sciences, 7, 195-205.
[18] H. Ding, C. Shu, K. S. Yeo and D. Xu (2006), 'Numerical Computation of Three-dimensional Incompressible Viscous Flows in the Primitive Variable Form by Local Multiquadric Differential Quadrature Method', Computer Methods in Applied Mechanics and Engineering, 195, 516-533.
Chinchapatnam et coll. [19] étudient l'équation non stationnaire de la diffusion par convection en une et deux dimensions pour différents nombres de Péclet par placement symétrique et asymétrique. Le schéma numérique utilise des fonctions radiales globales, telles que les multiquadratiques, les multiquadratiques inverses, les splines à plaques minces et les quintiques. Dans cette étude comparative, les auteurs concluent que la méthode symétrique n’est que légèrement meilleure que la méthode asymétrique.
et que pour les grands nombres de Péclet, une forte densité de nœuds est nécessaire pour obtenir une bonne approximation.
[19] Chinchapatnam, P.P., Djidjeli, K and Nair, P.B. (2006). Unsymmetric and symmetric meshless schemes for the unsteady convection–difusión equation. Computer Methods in Applied Mechanics and Engineering, 195, (19-22), 2432-2453.
Il existe peu de références, à notre connaissance, sur des algorithmes basés sur des fonctions radiales globales qui résolvent des problèmes d'analyse structurelle. Notamment, les travaux de Ferreira et al. [20] qui traite du problème de contrainte des poutres et plaques composites déformables, ainsi que les travaux de Zhang et al. [21] en élasticité plane. Récemment, Tiago et al. [22] utilisent la méthode de placement asymétrique utilisant différents noyaux radiaux pour résoudre et analyser des problèmes dans une dimension allant de l'élasticité linéaire statique, des vibrations libres et de l'analyse de la stabilité linéaire, aux problèmes physiques non linéaires de modèles endommagés.
[20] A. J. M. Ferreira, C. M. C. Roque, and P. A. L. S. Martins. Radial basis functions and higher-order shear deformation theories in the analysis of laminated composite beams and plates. Composite Structures, 66(1–4):287–293, 2004.
[21] X. Zhang, K. Z. Song, M. W. Lu, and X. Liu. Meshless methods based on collocation with radial basis functions. Computational Mechanics, 26(4):333–343, 2000.
[22] C. Tiago and V. Leitão, Application of radial basis functions to linear and non-linear structural analysis problems, Computers & Mathematics with Applications, 51(8), 1311-1334, 2006.

→Interpolation utilisant des fonctions radiales.
→Solution de l'équation de Poisson.
→Solution de l'équation de diffusion par convection.
→Décomposition de domaines avec fonctions radiales.
*Introduction à la programmation avec C++
* Programation orientée aux objets.
* Programmation générique.
* Programmation parallèle (MPI)
*Templates for the solution of linear systems.
Programmes pour résoudre l'équation de diffusion par convection
Diffusion par convection
Convection 2D pure, utilisant un placement non symétrique.
Matlab
Routine principale
Routine principale et auxiliaire (compressée)
C++
Ut + Ux + Uy =0
Principales routines
Méthode explicite, TPS+Pol grade 6
Méthode implicite TPS+Pol niveau 6
Méthode explicite Noyau multiquadratique
Routine principale et auxiliaire (compressée)
Convection - Diffusion 2D, utilisant un placement non symétrique.
Matlab
Routine principale
Routine principale et auxiliaire (compressée)
C++
Ut + mu*(Ux + Uy) = beta*grad(U)
Principales routines
Méthode implicite, TPS + Pol grade 6
Méthode de noyau multiquadrique implicite
Routine principale et auxiliaire (compressée)
Les étudiants de premier cycle et de troisième cycle sont invités à obtenir leur diplôme en résolvant des problèmes décrits en termes d'EDP en utilisant des techniques de calcul parallèle et des fonctions à base radiale, ainsi qu'en utilisant la bibliothèque développée à partir de ce projet.
Pour les sujets de thèse de premier cycle et de troisième cycle, veuillez contacter le Dr Pedro González Casanova (Instituto de Matemáticas, UNAM).
TEL: 56 22 47 47, OU ENVOYEZ-MOI UN EMAIL: casanova@matem.unam.mx
Lectures recommandées :
→ Wendland, H., Scattered Data Approximation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge, UK., 2005
→ G. E. Fasshauer, Meshfree Approximation Methods with Matlab Interdisciplinary Mathematical Sciences - Vol. 6 World Scientific Publishers, Singapore, 2007

Instituto de Matemáticas, UNAM

Université de Pau et des Pays de l'Adour | UPPA · Mathématiques Appliquées

(Paul Sabatier University - Toulouse III, Toulouse, France).

INFOTEC CDMX

Instituto de Geofísica, UNAM

(Laboratoire de Mathématiques de l'INSA de Rouen, EA 3226, France)

CUCSUR, Universidad de Guadalajara

INAOE
28 - 30 June 2011, New Forest, UK
A summer institute held 3–14 January 2011, Valparaiso, Chile
Andres Island, Colombia- March 2-7, 2008
TUNA::RBF. Dr. Luís Miguel de la Cruz, 28 de agosto 2008. Lugar: DGSCA.
El uso de patrones para el diseño de software científico
Dr. Gustavo Rodríguez Gómez, 4 de septiembre 2008. Lugar: DGSCA.